Data Structure--Binary search trees
Definition. A BST is a binary tree in symmetric order
A binary tree is either: ・Empty. ・Two disjoint binary trees (left and right).
Symmetric order. Each node has a key,
and every node’s key is: ・Larger than all keys in its left subtree. ・Smaller than all keys in its right subtree.
Java definition A BST is a reference to a root Node.
A Node is comprised of four fields:
- A key and A vaule.
- A reference to the left and right subtrees
1234567891011public class Node{private Key key;private Vaule val;private Node left,right;private int count;//for size()private Node(Key key,Vaule val){this.key=key;this.vaule=val;}}
BST implementation(Skeleton)
Get. Return Vaule corresponding to given key, or null if no such key.
Put .Associate value with key.(Tricky and recursive)
Search for key, then two cases:
・Key in tree ⇒ reset value.
・Key not in tree ⇒ add new node
Ordered Operations
-
如何求最大/最小值 ? 很简单,我们可以根据二叉查找树的定义,判定最左的子节点即为最小值,最右的为最大值。
-
如何写Floor和Ceiling 函数?(Floor. Largest key ≤ a given key.Ceiling. Smallest key ≥ a given key.) Q. How to find the floor / ceiling? Case 1. [k equals the key at root] The floor of k is k. Case 2. [k is less than the key at root] The floor of k is in the left subtree. Case 3. [k is greater than the key at root] The floor of k is in the right subtree (if there is any key ≤ k in right subtree); otherwise it is the key in the root.
12345678910111213141516171819public Key floor(Key k){Node X=floor(root,k);if (root == null) return null;return X.Key;}private Node floor(Node X,Key k){Node Y;if(X=null) return null;int cmp=k.compareTo(X.key);if(cmp<0)retrun Y=floor(X.left,k);else if(cmp==0) return X;else {if (floor(X.right,k)!=null)return floor(X.right,k);else return X;}} -
求数的大小: 方法:在每个节点存储字数节点个数的值,使用size函数,使得它返回该节点的count值,这样的话,节点必须新加一个变量count,size函数这么写:
1234567public class Node{private Key key;private Value val;private Node left;private Node right;private int count;}
这样put函数里应该多加这么一句:
- 迭代写法
方法,用队列实现,先存左边的node,再存root及节点,再存右边的节点。
- 算法比较
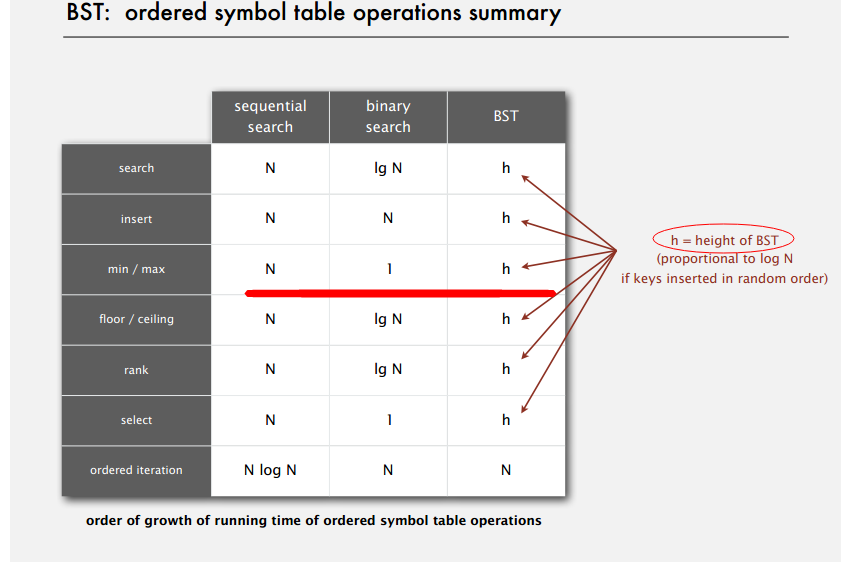 可见二叉查找树和二分查找的比较,二叉查找树算法复杂度与树的高度成正比,而二叉查找树树的高度又和二叉查找树的动态存储的数据结构,在插入方面更有优势(红线划到insert处)。
可见二叉查找树和二分查找的比较,二叉查找树算法复杂度与树的高度成正比,而二叉查找树树的高度又和二叉查找树的动态存储的数据结构,在插入方面更有优势(红线划到insert处)。

